 |
|---|
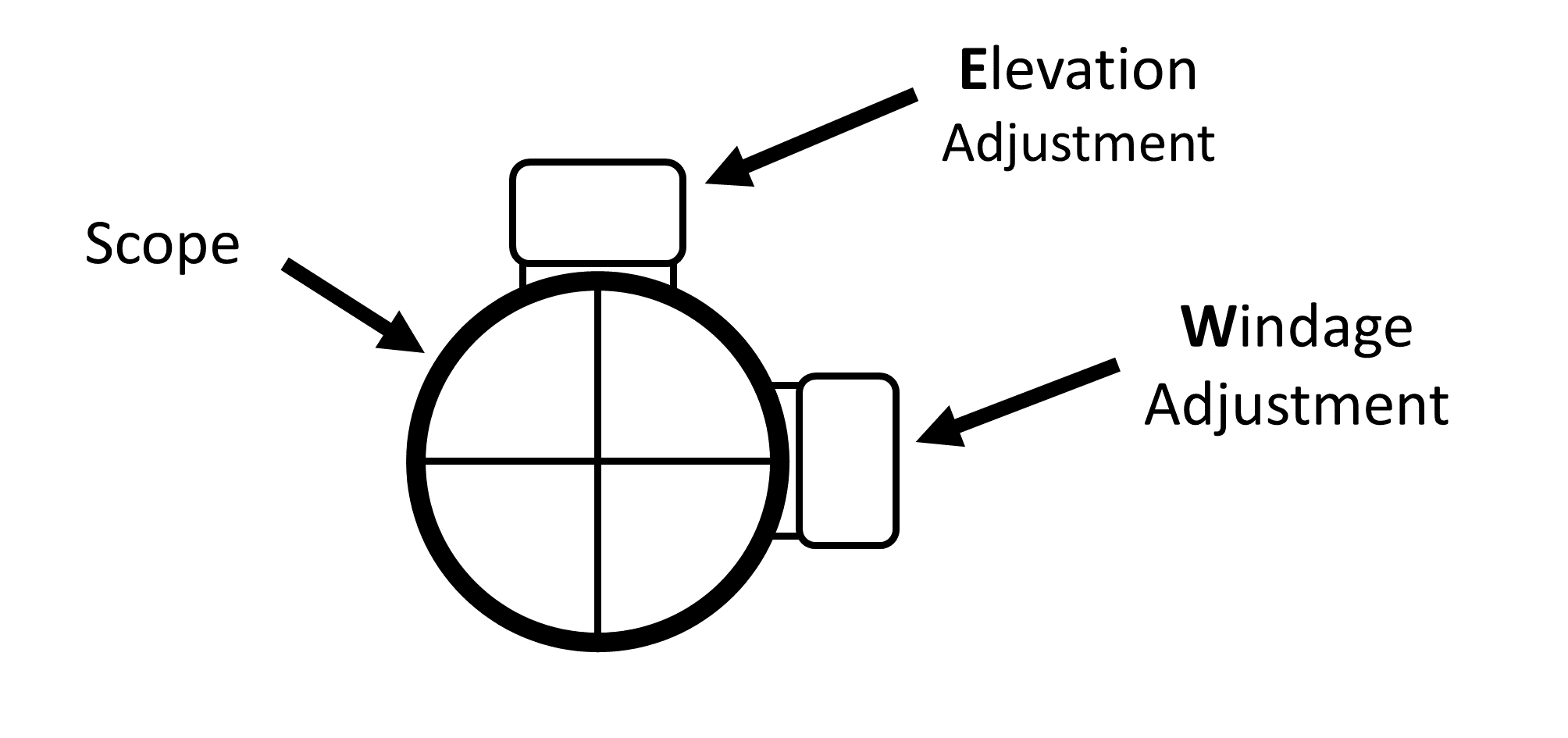
Elevation and Windage Information
Elevation and Windage
Elevation is the required up (U) and down (D) adjustment of the scope to hit the target. Windage is the required left (L) and right (R) adjustment of the scope to hit the target. The Elevation and Windage depends on the rifle setup, distance to the target, the wind, and the barrel angle, as well as less significant factors like air density (temperature, altitude), Gyroscopic spin drift, and the Coriolis force. The units of Elevation and Windage adjustment depends on the scope, but is typically given by minutes of angle (moa) or milliradian (mrad or mil). This rounds the value to the nearest 0.1 mrad or 0.25 moa increment. Be sure to choose the correct output units for your scope.
Note that: 1 mrad ≈ 10 cm @ 100 m
1 moa ≈ 1 in @ 100 yd
The distance from the muzzle of the barrel to the target.
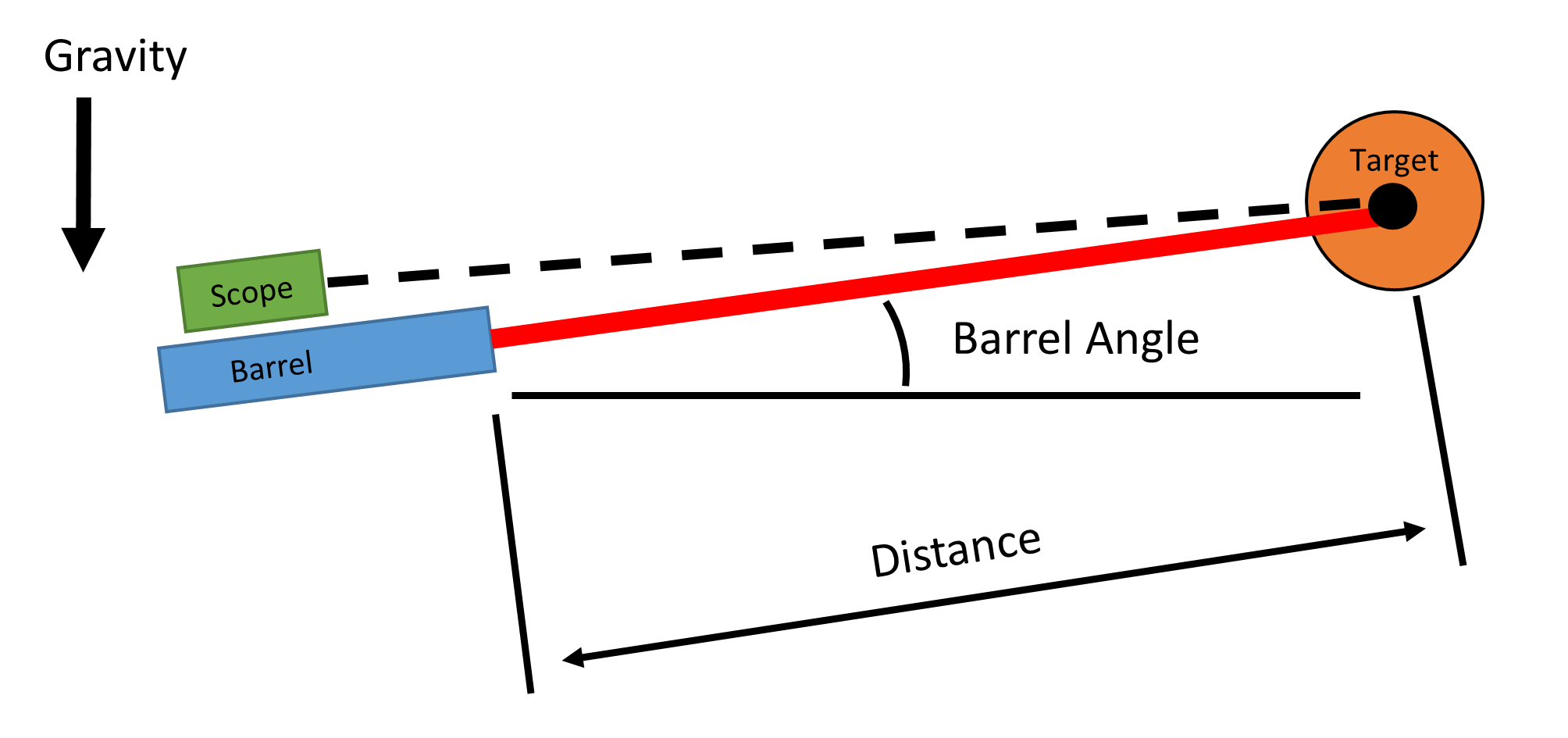
Barrel Angle
The barrel angle is measured from a flat shooting position (barrel perpendicular to the gravity vector). A good range finder will be able to give you this angle when you determine the distance to the target. Barrel angle sign is positive (+) when aiming upward to the target and negative (-) if you are aiming downward to the target. Make sure you include the negative sign (-) if the barrel is aiming downward.
Rifle Name
The rifle name is the name of the rifle setup you wish to use. The rifle setups are given by the setups saved using the basic rifle setup. This rifle setup gives all of the required information of the rifle, scope, and ammunition to calculate the elavation and windage. Make sure your rifle is setup and saved correctly with the correct units.
Wind Velocity
The wind velocity affects the trajectory of the bullet. The simplest way to measure the magnitude and direction of the wind is to split it into three components (three dimensions) in relation to the barrel direction. The x component (Wx) is considered along the axis of the barrel towards the target, the y component (Wy) is considered along the axis which is perpendicular to the barrel and the gravity vector, and the z component (Wz) is considered along the axis which is perpendicular to the barrel axis (x axis) and perpendicular to the y axis. Given these axes the wind can easily be determined in these directions using an anemometer.
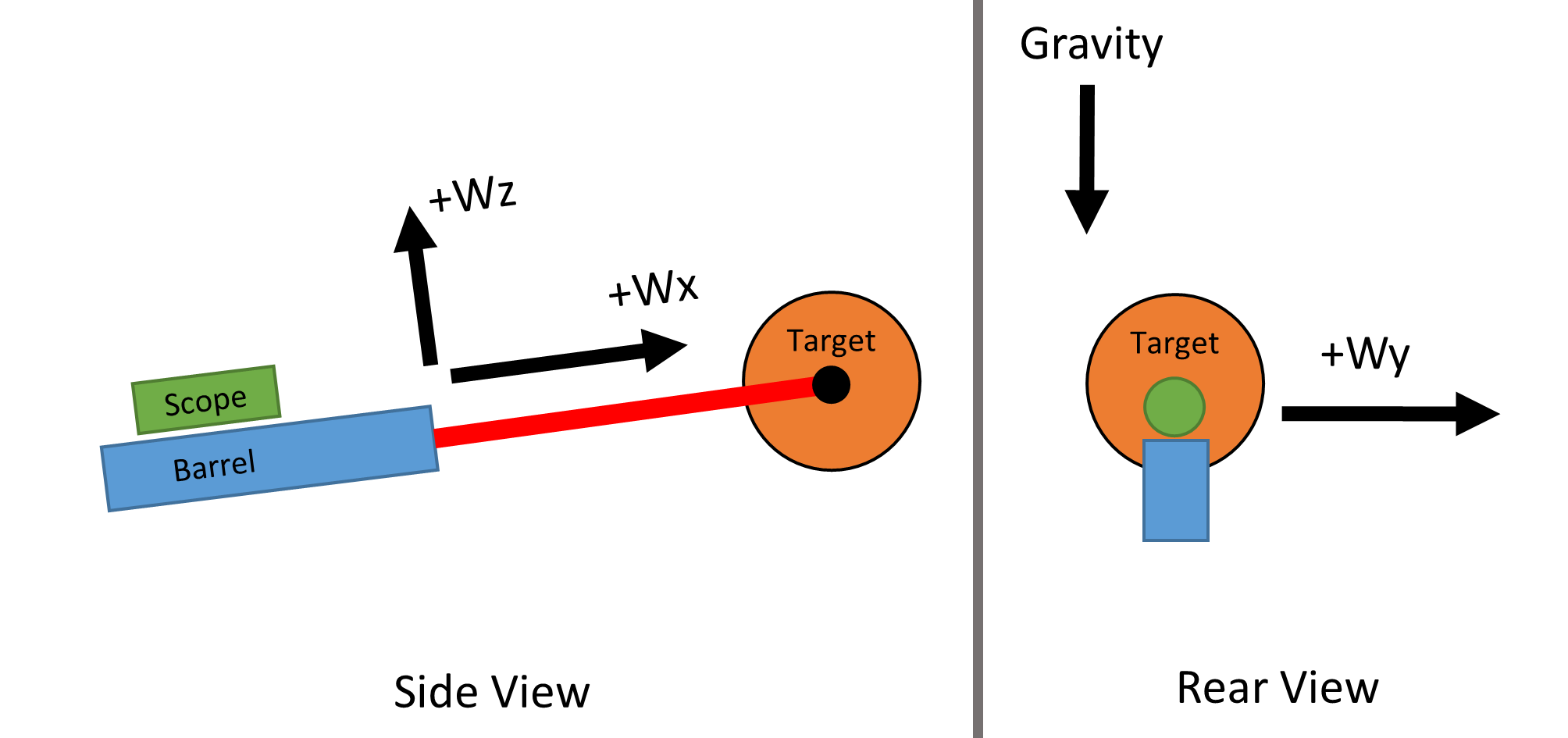
Wx (Wind in the x direction)
Wind in the x direction (Wx) is considered along the axis of the barrel towards the target. Wx sign is positive (+) when the wind direction is from the rifle to the target and negative (-) if the wind direction is from the target to the rifle. Make sure you include the negative sign (-) if the wind is in the negative direction.
Wy (Wind in the y direction)
Wind in the y direction (Wy) is considered along the axis which is perpendicular to the barrel and perpendicular to the gravity vector. Wy sign is positive (+) when wind is to the right (when looking towards the target) and negative (-) if the wind direction is to the left. Make sure you include the negative sign (-) if the wind is directed to the left.
Wz (Wind in the z direction)
Wind in the z direction (Wz) is considered along the axis which is perpendicular to the barrel axis (x axis) and perpendicular to the y axis. Wz sign is positive (+) when wind direction is upwards and negative (-) if the wind direction is downward. Make sure you include the negative sign (-) if the wind is directed downwards.
Advanced
Air Density
The density of the air influences the drag of the bullet. The affect of temperature and altitude on the bullet trajectory is captured by the air density. The air density is given by the air temperature, pressure, and humidity. To calculate air density use the air density calculator provided (see extra tools). The influence of the humidity on the density generally results in a negligible change in bullet trajectory; thus, you may wish to guess the humidity (0% to 100%) or use a 0% relative humidity (dry air assumption).
Spin Drift
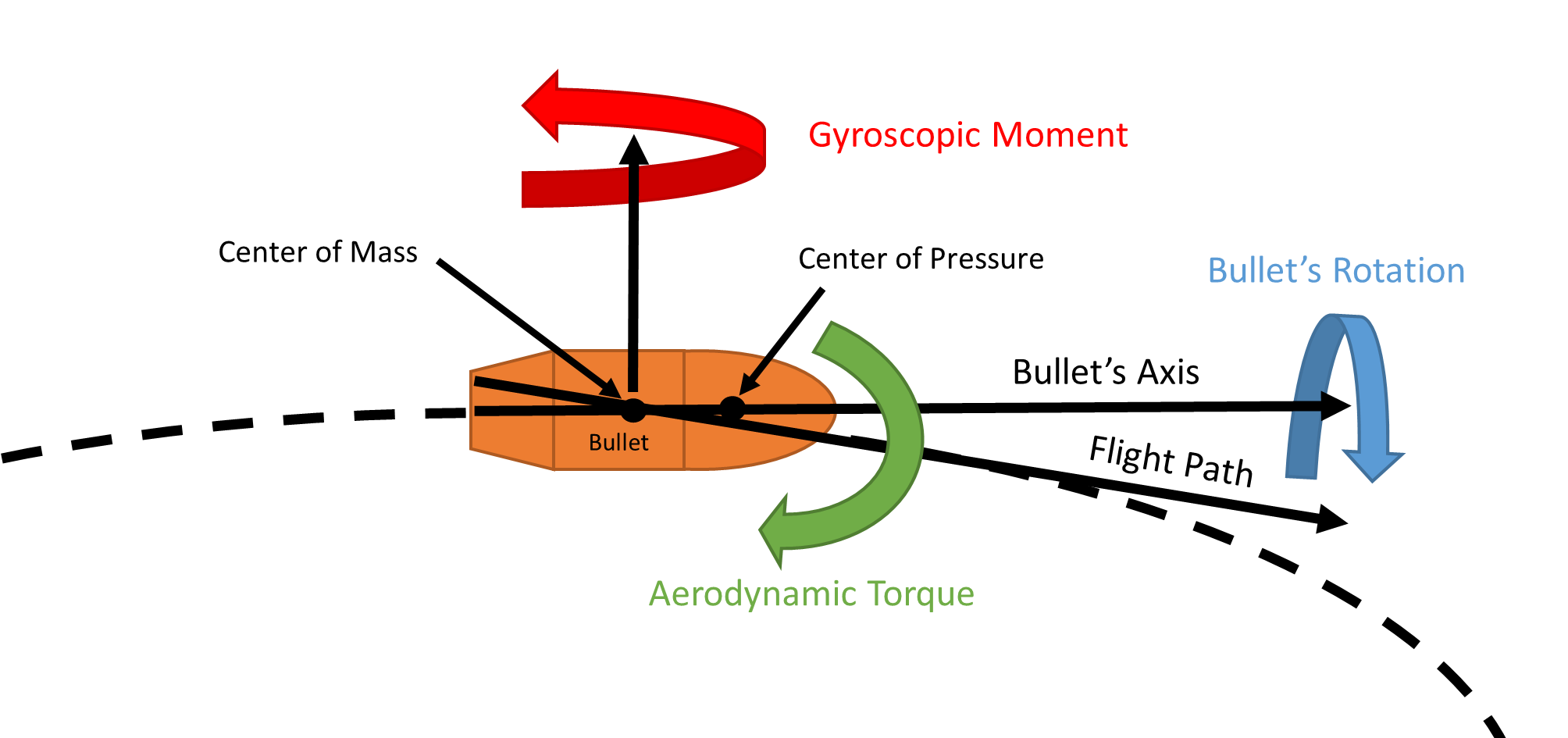
Gyroscopic spin drift occurs because of the aerodynamic torque applied to the spinning bullet. Gravity means that the trajectory of the bullet is not straight. As the bullet is in flight its direction is changed towards alignment with its flight path because of the aerodynamic forces (drag). The net aerodynamic force act on through center of pressure of the bullet, which is in an different location that the bullets center of mass, resulting in a torque force applied to the bullet. The torque on the spinning bullet results in the gyroscopic effect, which results in a moment in the axis which is perpindicular to the bullet direction and the applied torque axis. The results of this is simple, if the bullet spins to the right (clockwise) then the bullet drifts to the right and vise versa. To calculate the spin drift a empirical formula was developed which uses the Millar stability factor. This requires knowleage of the bullet mass, bullet diameter, bullet length, and barrel rifling (twist rate and direction). The spin drift is often small, and only presents itself at long ranges.
Coriolis Force
The Coriolis force is an inertial force that acts on the bullet because its motion is relative to a rotating reference frame (the earth spinning). The Coriolis force results in an acceleration of the bullet where the direction and magnitude of the acceleration depends on the bearing (cardinal direction - e.g. West - 270 degrees) of the bullet path and the locations latitude. Make sure you specify the correct hemisphere in the units (North - N, South - S).